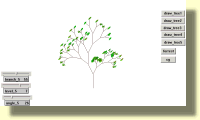
Draws fractal trees
to tree :distance
if :distance < minimum [stop]
forward :distance
right angle
tree :distance - step
left (angle * 2)
tree :distance - step
right angle
back :distance
end
trees4.zip 21KB ![]() use winzip to unzip
use winzip to unzip
Draws fractal trees
Based on code By David Dimsey
Ivanhoe Grammar School Plenty Campus
fractals1.zip 11KB ![]() use winzip to unzip
use winzip to unzip
Draws fractal trees
to tree procedure modified from original found at: http://www.microworlds.com/library/math/recursive/index.html
to tree :length :ang :st
if :length < :st [stop]
; halt when branch
;
length is less than st
fd :length
lt :ang
tree :length / 2 :ang :st ;
recursive call
rt :ang
tree :length / 2 :ang :st ;
recursive call
rt :ang
tree :length / 2 :ang :st ;
recursive call
lt :ang
bk :length
end
August 11, 2004
seth random 360
pu
bk 100
setc (random 9900) + 10 pd
sierpinski s_size
end
to rtriangle :size
fd :size
rt 135
fd (sqrt 2)* :size
rt 135
fd :size
rt 90
end
to hole :size
fd :size / 2
rt 90
fd :size / 2
rt 90
rtriangle :size / 2
pu
rt 45
fd :size / 4
pd
fill
bk :size / 4
rt 45
fd :size / 2
rt 90
bk :size / 2
end
to sierpinski :size
rtriangle :size
hole :size
if :size > 15 [sierpinski :size / 2]
fd :size / 2
if :size > 15 [sierpinski :size / 2]
bk :size / 2
rt 90
fd :size / 2
lt 90
if :size > 15 [sierpinski :size / 2]
lt 90
fd :size / 2
rt 90
end
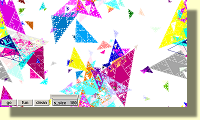
sierpinski2.mw2 111 KB
sierpinski2.zip 8KB ![]() use winzip to unzip
use winzip to unzip
www.microworlds.com/library/math/sierpinski/resources.htm
to
sierpinski
pd
seth 0
rt 30
draw_shape 200 6
end
to draw_shape :size :level
if :level < 1 [stop] ;
stopping rule
repeat 3 [
draw_shape :size / 2 :level - 1 ;
recursive call
fd :size
rt 120]
end
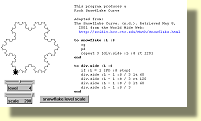
to curve
pd
seth 0
rt 30
curve_shape 150 6.5
end
to curve_shape :size :level
if :level < 1 [stop] ;
stopping rule
repeat 4 [
fd 0.75 * :size
rt 180
curve_shape :size / 2 :level - 1 ;
recursive call
rt 180
fd 0.25 * :size
rt 90
]
end
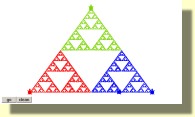
October 8, 2004
sierpinski3.mw2
43 KB
sierpinski3.zip 21 KB
sierpinski3.exe 84 KB
GNU License.txt
![]()
set.up.triangle
t1, setc "red
t2, setc "blue
t3, setc "green
forever [step]
end
to set.up.triangle
t1, setpos [-250 -165]
t2, setpos [250 -165]
t3, setpos [0 180]
t4, pu st
end
to step
make "random.vertex ((random 3) + 1)
make "random_vertex_turtle word "t :random.vertex
talkto :random_vertex_turtle
; setc color + 1 ; change the colour of the active vertex
make "p pos
talkto "t4
towards :random_vertex_turtle
if :random_vertex_turtle = "t1 [setc "red]
if :random_vertex_turtle = "t2 [setc "blue]
if :random_vertex_turtle = "t3 [setc "green]
make "q pos
make "distance sqrt((power ((first :p) - (first
:q)) 2) + (power ((last :p) - (last :q)) 2))
fd 0.5 * :distance
pd fd 0
pu
end

October 8, 2004
sierpinski4.mw2
51 KB
sierpinski4.zip 14 KB
sierpinski4.exe 76 KB
GNU License.txt
![]()
From THE
FRACTAL UMBRELLA
http://www.maths.adelaide.edu.au/people/pscott/fractals/
ht
cg
Sieve -160 -160 400 level
end
to
Sieve :x :y :size :level
if :level = 0 [triangle :x :y :size stop]
Sieve :x :y :size / 2 :level - 1
Sieve :x + :size / 2 :y :size / 2 :level - 1
Sieve :x + :size / 4 :y + :size * 0.433
:size / 2 :level - 1
end
to triangle :x :y :size
pu setx :x sety :y seth 30 pd
repeat 3 [fd :size rt 120]
pu setx :x + :size / 2 sety :y + 2 pd
; add some colour
setc (random 7) + 100
fill
setc "black
end
sierpinski5.mw2
51 KB
sierpinski5.zip 14 KB
sierpinski5.exe 76 KB
GNU License.txt
![]()
From THE
FRACTAL UMBRELLA
http://www.maths.adelaide.edu.au/people/pscott/fractals/
output first :p
end
to y :p
;output item 2 :p
output last :p
end
to scale_triangle :p
output se (x :p) * scale - scale / 2 (y :p) * scale - scale / 2
end
to triangle :p1 :p2 :p3
pu
setpos scale_triangle :p1
pd
setpos scale_triangle :p2
setpos scale_triangle :p3
setpos scale_triangle :p1
end
to rule :n :p
if :n = 1 [output se (x :p) / 2 (y :p) / 2]
if :n = 2 [output se (x :p) / 2 + 0.5 (y :p) / 2]
if :n = 3 [output se (x :p) / 2 + 0.25 (y :p) / 2 + 0.5]
end
to ifs :p1 :p2 :p3 :level
if :level = 0 [triangle :p1 :p2 :p3 stop]
ifs rule 1 :p1 rule 1 :p2 rule 1 :p3 :level - 1
ifs rule 2 :p1 rule 2 :p2 rule 2 :p3 :level - 1
ifs rule 3 :p1 rule 3 :p2 rule 3 :p3 :level - 1
end
to go
ht
cc
cg IFS [0 0] [1 0] [0.5 1] level
end
mandelbrot01.mw2
51 KB
mandelbrot01.zip 22 KB
mandelbrot01.exe 84 KB
A work in progress no comments as yet.
This version is very slow see version 0.2 for a much faster version. That uses recursion.
Based on SmallBASIC code by Jeff Fox
http://smallbasic.sourceforge.net/scode/vsrc.php?show=33

August 21, 2004
mandelbrot02.mw2
57 KB
mandelbrot02.zip 26 KB
mandelbrot02.exe 88 KB
Version 0.2 much faster than version 0.1
Uses a recursive call with bailout checking.
Based on SmallBASIC code by Jeff Fox
http://smallbasic.sourceforge.net/scode/vsrc.php?show=33
August 21, 2004
mandelbrot03.mw2
225 KB
mandelbrot03.zip 87 KB
mandelbrot03.exe 184 KB
Generates a Mandelbrot Set
Version 0.3 faster than version 0.2
Plots from the top and bottom at the same time
Fixed a problems with the :x_scale
Based on SmallBASIC code by Jeff Fox
http://smallbasic.sourceforge.net/scode/vsrc.php?show=33
The_King's_Dream.mw2
190 KB
The_King's_Dream.zip 46
KB
The_King's_Dream.exe 108
KB
![]() Plugin version
Plugin version
GNU License.txt
![]()

by Dr Clifford Pickover
The book Chaos in Wonderland just came out in paperback, and I thought
some of you would like a computer recipe from the book. The book is a
blend of science fiction, graphics, mathematics, astronomy, computer graphics,
and fractals to introduce the reader to chaos science -- the science behind
many intricate, unpredictable patterns in mathematics and nature.
Pickover, C. (1995) Chaos in Wonderland: Visual Adventures
in a Fractal World. St Martin's Press: New York. ISBN 0-312-12774-X
x = 0.1; y = 0.1; /* starting point */
DO 10 Million Times
xnew = sin(y*b) + c*sin(x*b)
ynew = sin(x*a) + d*sin(y*a)
x = xnew; y = ynew; PlotDotAt (x, y)
END
The values of the real number constants a, b, c, and
d may be chosen at random in a range (-3 < a,b < 3) and (0.5 <
c, d < 1.5 ). These simple systems generate information as the system
evolves. To see the patterns unfold, use the rules and starting conditions,
repeat the equations over and over again, stand back, and watch the visually
exciting behavior evolve on the computer screen. Each new value of x and
y determines the position of points on a plane.
To produce the King's beautiful fractal dream, use the following constants: (a = -0.966918, b = 2.879879, c = 0.765145, and d = 0.744728). The picture boundaries are (-1.86 < x < 1.86) and (-1.51 < y < 1.51) . The Lyapunov exponent, which is explained in detail in the book, characterizes the degree of chaos in the pattern. For the King's dream, the value of the Lyapunov exponent is 0.48. If you magnify the center of the pattern, you will find additional intricate plumage.
http://www.geocities.com/CapeCanaveral/Launchpad/5113/fr40.htm
to dream
cg
pu
ht
make "x 0.1
make "y 0.1
make "a -0.966918
make "b 2.879879
make "c 0.765145
make "d 0.744728
make "scale 200
repeat 100000 [
make "xnew sin(:y * :b) + :c
* sin (:x * :b)
make "ynew sin(:x * :a) + :d
* sin(:y * :a)
make "x :xnew * :scale
make "y :ynew * :scale
setx :x
sety :y
pd
fd 0 ;
draw a point without moving the turtle
pu
]
end

October 8, 2004
dragon1.mw2
34 KB
dragon1.zip 11 KB
dragon1.exe 72 KB
![]() Plugin version
Plugin version
GNU License.txt
![]()
From THE
FRACTAL UMBRELLA
http://www.maths.adelaide.edu.au/people/pscott/fractals/
ht
cg
pu
fd 50
pd
dragon 200 level
end
to Dragon1 :size :level
if :level = 0 [fd :size stop]
Dragon :size * 0.707 :level - 1
lt 90
Dragon1 :size * 0.707 :level - 1
end
to Dragon :size :level
pd
if :level = 0 [fd :size stop]
Dragon :size * 0.707 :level - 1
rt 90
Dragon1 :size * 0.707 :level - 1
end
IFS10.mw2 33KB
IFS10.zip 17 KB
IFS10.exe 80KB
![]() Plugin version
Plugin version
GNU License.txt
![]()
From THE
FRACTAL UMBRELLA
http://www.maths.adelaide.edu.au/people/pscott/fractals/
to dot
ht
make "scale IFS_sz ; IFS_sz is a slider range 1 - 400
; setc (random 5) + 100
; add some colour
; setc "black ; or stick to Black
; note the colours are currently
; set in the ChooseRule procedure
setx :x * :scale
sety :y * :scale - (:scale / 2)
pd
fd 0
pu
end
to rule1
; Xn+1 = AXn + BYn + C
; Yn+1 = DXn + EYn + F
make "a 0
make "b 0
make "c 0
make "d 0
make "e 0.16
make "f 0
make "t (:a * :x) + (:b * :y) + :c
make "y (:d * :x) + (:e * :y) + :f
make "x :t
end
to rule2
make "a 0.85
make "b 0.04
make "c 0
make "d -0.04
make "e 0.85
make "f 0.16
make "t (:a * :x) + (:b * :y) + :c
make "y (:d * :x) + (:e * :y) + :f
make "x :t
end
to rule3
make "a 0.2
make "b -0.26
make "c 0
make "d 0.23
make "e 0.22
make "f 0.16
make "t (:a * :x) + (:b * :y) + :c
make "y (:d * :x) + (:e * :y) + :f
make "x :t
end
to rule4
make "a -0.15
make "b 0.28
make "c 0
make "d 0.26
make "e 0.24
make "f 0.08
make "t (:a * :x) + (:b * :y) + :c
make "y (:d * :x) + (:e * :y) + :f
make "x :t
end
to ChooseRule
; chose a rule based on its probability
make "r random 100
if :r = 0 [setc "red rule1 stop]
if :r < 83 [setc "green rule2 stop]
if :r < 92 [setc "blue rule3 stop]
setc "black rule4
end
to IFS :n
pu
make "x 0
make "y 0
repeat :n [ChooseRule dot]
end